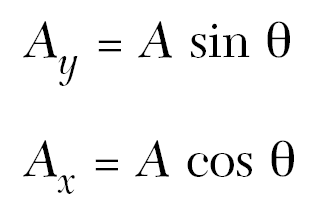The football has 2 velocities.
Which velocity is the football player matching.

 

 

 

 

Horizontal velocity.
The football and the football player
have a constant horizontal velocity.

 

 

St. Mary's Show Me The Physics

 

 

Ex) A projectile leaves ground at an angle of 60.° and a speed of 100.m/s.

(a) Find the objects maximum height & total time in the air

(level ground)

 

Ex) A projectile leaves ground at an angle of 60.° and a speed of  100. m/s.

 

First find the initial vertical component of the object's velocity 

 

Ө = 60.°

 

Vi  = 100. m/s
Viy = ?

 

 

Viy = Vi(sinӨ)

 

 

= (100. m/s)sin60.°

 

 

 

 

Viy = 87. m/s up

 

 

 

 

 

(b) Find the objects maximum height.

 

Viy = 87. m/s
ay = -10. m/s2 (ascending)
dy (max) =?
Vfy = 0 (at max height)

 

 

Vf2 = Viy2 + 2ad

 

 

02 = (87. m/s)2 + 2(-10. m/s2)d

 

0 = 7569 + -20.dy

 

 

subtract 7569 from both sides

 

 

-7569 = -20.(dy)

 

 

dy = 378 m

 

 

Actually ......

 

 

 

dy = 380 m

 

 

(2 sig. figs)

 

(b) Total time in the air

Viy = 87. m/s up

 

t = 2(87 m/s)/9.8 m/s2

 

t = 18 sec


 

 

 

 

ex) A rock is thrown from a cliff with initial speed of 40. m/s at an angle of 45.° below  the horizontal. 

(a) If rock strikes ground in 1 sec, height of cliff?

a) What is the vertical component  of the initial velocity?

Ө = 45.°

 
Vi = 40. m/s
Viy = ?     
 
Viy = VsinӨ
 
= (40. m/s)sin45.° 

			
 

			
Viy = 28 m/s down 

		

		
 

		
 

		

		 

		

		 

		

		 

		

		 

		
 

		
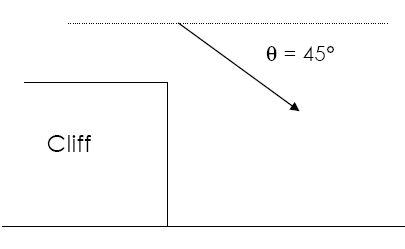
(b) If the 
		rock strikes ground in 1.0 sec what 
		is 
		height of cliff?

		
 

		
 

		
dy = ? 
		(height)

		
ay = + 10. m/s2

		
 

		
t = 1.0 sec

		
 

		
Viy = 28 m/s
		(from before)

		

		
 

		
 

		
 

		

			

		
dy = Viyt + (˝)at2

			

		

		
 

		
 

		
 

		
 

		
 

		

			

				
= 28.m/s(1sec)+˝(10. m/s2)(1.0sec)2

			

		

		
 

		
 

		
 

		
28 m + 5.0 m

		
 

		

		
 

		
dy = 33 m down

		

		
 

		
 

		

		
 

		
 

		

		

		 

		

		

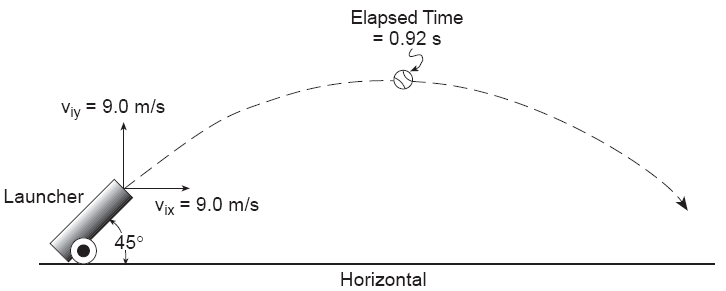
		At Peak,

		
 

		
 Vx 
		= ?

		
 

		
 

		
 

		

		
Vx 
		= 9.0 m/s

		
 

		

		 

		

		

		
 

		
 

		
h

		

		Total Time in Air?

		

		 

		

		 

		

		 

		

		1.84 sec 

		(twice peak)

		

		 

		

		 

		

		actually 1.8 

		

		 

		

		 

		

		 

		

		(2 sig. figs.)

		

		 

		

		 

		

		

		

		 

		

		 

		

		 

		

		

		

		
What will the horizontal velocity of the baseball be 
		just before it hits the ground?

		
 

		
 

		
 

		
 

		
9 m/s, Vx is constant

		
 

		

		Ex) A wild bowler releases the his bowling ball at a
		speed of 15 m/s and an
		angle of 34.0 degrees above the 
		horizontal. 

		

		 

		

		Calculate the horizontal distance that the bowling ball 
		travels if it leaves the bowlers hand at a height of
		2.20 m above the ground.

		

		 

		

		 

		

		dx = Vxt = Vcosqt

		

		 

		

		Need to find t

		

		 

		
dy = Viyt + (˝)at2

		

		
Viy = Vsinq

		
Viy = 8.6 m/s

		
 

		
dy = Viyt + (˝)at2

		
 

			

		
2.20 m = (-8.6m/s)t + 4.9t2

		
0 = 4.9t2 +(-8.6m/s)t - 2.20m

				
 

				
Quadratic Equation

				

				
t = 1.99 s, -0.225 s

		

		

		 

		

		dx = Vxt = Vcosqt

		

		

		

		dx = Vxt 

		

		 

		

		= (15m/s)cos34(1.99 sec)

		

		 

		

		=  25.6 m

		

		 

		

		The ammunition fired from an M-16 rifle has a muzzle velocity of 1000 
		m/s. A sniper perched on a tower 50 m high aims at a target and fires. 

		

		(A) The sniper aims her rifle 53.1 degrees above 
		the horizontal. How far away from the platform does the bullet hit the 
		ground? 

		

		Neglect air resistance. 

		

		 

		

		Vx = VcosӨ = 600 m/s

		

		dx = VcosӨt = [600m/s]t =

		

		 

		

		Need to find t

		

		 

		

		Make down positive

		

		Δdy = -VsinӨt + 1/2gt2

		

		50 m = -1000m/s[sin53.1]t + 4.9t2

		

		50 m = -800t + 4.9t2

		

		 0 = 4.9t2 - 800t - 50. m

		

		 

		

		t = 163 sec

		

		 

		

		Vx = VcosӨ = 600 m/s

		

		dx = VcosӨt = [600m/s]t =

		

		 

		

		dx = 98000 m

		

		 

		

		(B) With what speed would the bullet hit? 

		

		Vx = 600 m/s

		

		down Neg.

		

		Vfy = -VsinӨ + gt

		

		Vfy = -800m/s + 10m/s2(163sec)

		

		Vfy = 830 m/s

		

		 

		

		Pythagorean Theorem

		

		 

		

		V = 1000 m/s

		

		 

		

		(C) If the target is 500 meters away on a platform 
		50 meters high, what angle would the sniper have to make with her gun to 
		hit the target? 

		

		 

		

		Dx = Vxt

		

		500 m = [(1000m/s)cosӨ]t

		

		 

		

		Δdy = Viyt + (˝)at2

		

		 

		

		0 = Viyt + (˝)at2

		

		0 = VsinӨt + 5t2

		

		 

		

		

		

		 

		

		 

		

		 

		

		 

		

		 

		

		(A) 98000 m (B) 1000 m/s (C) 44.9 

		

		 

		

		

		

		

		
		Monkey and 
		Hunter

		 Don Ion 

		

		(offsite)

		

		 

		

		

		

		 

		

		 Flash 
		Physics

		 Don Ion 

		

		 

		

		

		

		 

		


		

		

		St. 
		Mary's U. Astronomy and Physics Dept.

		

		|
		Onsite 
		|

		

		 

		

		

		

		 

		

		 

		

		

		

		 

		

		 

		

		 

		

		 

		

		

		

		 

		

		

		

		 

		

		 

		

			

				
		
		
			

		

		

		
		Projectile Motion Game

		St. Mary's Physics

		

		 

		

		 

		

		 

		

		 

		

		

		

		

		

		

		

		

		 

		

		 

				

		ŠTony Mangiacapre., 
		- All Rights Reserved [Home]
			
		Established 1995

		Use any material on this site (w/ attribution)