![]()
![]()
2nd Law - Relationship between F, m, a
Unbalanced forces
cause objects to accelerate:
ΣFnet = ma
Fnet = Resultant
![]()
Ex) Mass M below is lifted up with an acceleration a. Find the tension in the string T

ΣFnet = ma
(up positive)

T - mg = ma
T = ma + mg
String Pulled up
T = m(g + a)
String Acelerated down?
T = m(g - a)
Two masses are connected by a string.
Find tension force on top and bottom rope.

Ex 1) Two masses are connected by a string and remain at rest.
Find tension force on top and bottom rope.

SF = 0
Top String Tension Force
TA - mag - mbg = 0
TA = mag + mbg
Bottom String Tension Force
TB - mbg = 0
TB = mBg
Ex 2) Find the tension of top and bottom string if objects accelerated upward
Free body diagram B (easier)
Sketch all forces on A

Force of tension on B (easier)
Free body diagram B
Sketch all forces on B
SF = mBa
TB - mBg = mBa
TB = mBa + mBg
= (force of accel. of B + weight of B)
Sketch all forces on A
SF = mAa
TA - TB - mAg = mAa
TA = mAa + mAg + TB
Since TB = mBa + mBg
TA = mAa + mAg +mBa+mBg)
TA=(mAa+mBa)+(mBg+mAg)
= (force of accel) + (weights)
Giancoli p. 98) 8, 25

 |
"Which cart is slowing down as it travels to the right?" |
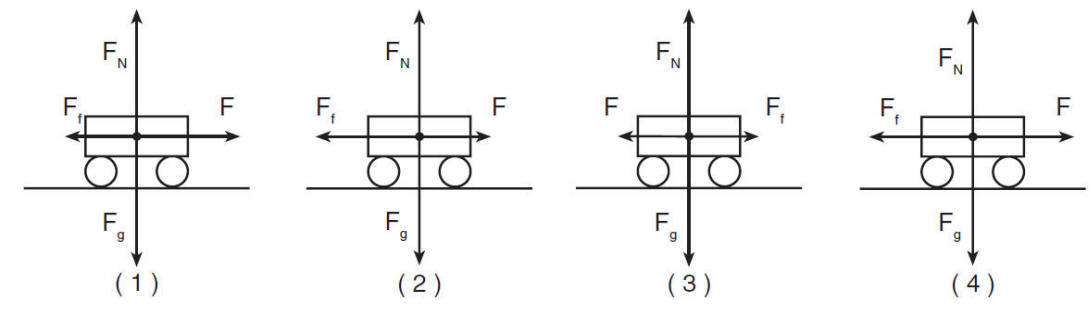
Choice 2

![]()
![]()
Check out this
Video at Georgia Pacific Broadcasting
![]()
©Tony Mangiacapre., - All Rights
Reserved [Home]
Established 1995
Use any material on this site (w/ attribution)